差分约束
差分约束系统。
2022-03-30发布,
2022-06-03再修。
我们经常会遇到一些问题,就是给出一堆未知量,再给出一堆类似“某一个未知量比另一个未知量最多(最少)大(小)多少”的问题,让我们从这一团繁杂的毛钱中拎出一根线头来,以求得这个毛线团的一组可行解。
比如说下面这个东西:
$$
\begin{cases}
x_1 \geq x_2 - 10 \\
x_1 \leq x_3 - 20 \\
x_3 \leq x_2 + 10 \\
x_4 \leq x_3 - 10 \\
x_2 \leq x_4 - 10
\end{cases}
$$
我们就基本上无从下手。
这时候,我们就需要引入一个新的算法——差分约束。
差分约束通过将不等式的问题转化为最短路(或最长路)问题来求解。
最短路?为什么?
回忆我们学习最短路的时候学到的知识。
假设对于两个点 $a$ 和 $b$,如果其间有一条边长为 $w$ 的有向边 $a \to b$,那么它们的 $dis$ 一定满足 $dis[b] \leq dis[a] + w$。
我们如果将每一个未知量 $x_k$ 与每一个点的 $dis[i]$ 联系起来的话,那么我们就可以得到形如 $x_b \leq x_a + w$ 的一堆不等式。
而我们刚好需要这些不等式。
于是我们就可以将我们手中的不等式组转化为一堆边,并将其放到图里面,建成一个有向图。
最后得出的每一组合法的最短距离,都对应了一组不等式组的解。
我们首先把所有的式子转化为 $x_u \leq x_v + w$ 的形式,再从每一个 $v$ 向 $u$ 建一条边权为 $w$ 的有向边。
这个有向图可以有环,毕竟环是不影响我们的求值环节的。
但是它不能有负环。
比如说下面这一组边:
$$
\begin{cases}
x_2 \leq x_1 + 10 \\
x_3 \leq x_2 + 10 \\
x_1 \leq x_3 - 30
\end{cases}
$$
建到图上就是这个样子:
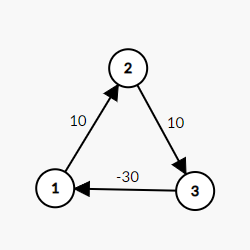
根据原始的不等式组,最终我们会得到 $x_1 \leq x_1 - 10$ 这样一个奇怪的式子,从而导致不等式组无解。
从图上看,这三条边构成了一个负环。
所以说,一个负环最终会导致出现一些奇怪的不等式,最终导致不等式组无解。
(当然,如果使用的是最长路的话就是正环)
那我们怎么判负环?(或者说正环)
SPFA!
(SPFA信徒狂喜)
实现
但是我们光靠这些边实际上是不能得出最终解的。
很多情况下,这张图根本不联通。
但是这样的图还是可以找到至少一组可行解的。
所以我们还需要建一个超级源点,向每一个点连一条长度为0的边。
应用
具体情况下,我们不仅有类似 $x_a \leq x_b + w$ 这样的式子,还有其他的一些奇奇怪怪的约束条件。
下面列出了一些常见的约束条件和解决办法:
| 约束条件 | 解决办法 |
|---|---|
| $x_a \leq w$ | 将源点到 $a$ 的边权从0改到 $w$。 |
| $x_a \geq w$ | 从 $a$ 向源点连一条长为 $-w$ 的边。 |
| $x_a = x_b + w$ | 将其拆分为 $x_a \leq x_b + w$ 和 $x_b \leq x_a + (-w)$。 |
| $x_a + x_b \leq w$ | 差分约束会寄。请注意一下题目中有没有可以利用的其他特殊性质。 |
如果在一个不等式组的约束下(不等式组有解),想求出 $x_i − x_j$ 的最大值呢?
首先一定有 $x_i − x_j \leq j$ 到 $i$ 的”最短” 路 $\operatorname{dis}(j,i)$ 。因为我可以先走到 $j$ ,然后走“$j$ 到 $i$ 的”最短路””到 $i$ 。
然后我们证明 $x_i − x_j$ 可以取到这个值。
这相当于往不等式组中添加一个 $x_i − x_j \geq \operatorname{dis}(j,i)$ ,如果不等式组仍有解,$x_i − x_j$ 就能取到 $\operatorname{dis}(j,i)$ 。
这也相当于在图中添加一条边,从 $i$ 到 $j$ ,边权是 $−\operatorname{dis}(j,i)$ 。这样加边一定不会出现负环,因为 $\operatorname{dis}(j,i)$ 是 $j$ 到 $i$ 的最短路,要有负环的话就有别的路径长度 $< \operatorname{dis}(j,i)$ 了。
如果要求 $x_i − x_j$ 的最小值,就是求 $x_j − x_i$ 的最大值的相反数,即 $−\operatorname{dis}(i,j)$。
“$x_i − x_j$ 的最小值”$\leq$“$x_i − x_j$ 的最大值”,对应了 $−\operatorname{dis}(i,j) \leq \operatorname{dis}(j,i)$ ,也就是 $\operatorname{dis}(i,j) + \operatorname{dis}(j,i) \geq 0$ ,也就对应了图中没有包含 $i,j$ 的负环。
代码
洛谷板子题
参考代码:Luogu P5960
例题
其实差分约束最难的地方不是跑最短路求解的过程,而是如何去建这个图。
这样子的话其实是与网络流有些类似的情况的,有时候我们没有很好的办法来把我们题目中给出的信息来转化成为我们的建图方式。
下面首先会放上两道比较简单的、朴素的题目,没有什么太难理解的地方;然后就会放一些转化题意的例子。
Luogu P1993 小 K 的农场
题目链接:Luogu
接近板子题。
我们可以使用我们刚刚学到的技巧来完成这道题目。
参考代码:Luogu P1993
Luogu P3275 [SCOI2011] 糖果
题目链接:Luogu || AcWing || LibreOJ
我们遇到了新的约束条件:不带取等的不等式。
我们看一下题目的条件:分糖果。
由于糖果是一块一块的,我们不能分给小朋友们 $m=\dfrac{1}{2}$ 块糖果或 $\lim\limits_{m \to 0} m$ 块糖果,所以我们可以尝试着更改一下约束条件。
我们可以将 $x_a > x_b$ 改为 $x_a \geq x_b + 1$。
这样就可以建图了。
(20220714更新)
现在洛谷上面加入了一点Hack数据,会卡掉较慢的SPFA算法,而原题中SPFA是可以过的。(但是数据范围给的是 $10^5$)
这道题的本意应该是让我们利用tarjan算法及进行缩点之后再跑差分约束。
我们看看怎么缩点。
我们尝试将所有的环缩成一个点,而这个环内的所有点的值都会相等。
那么我们可以确定,环上只含有1、3、5三种类型的边。
(因为你看:我们建出来的图是一个有向图,如果其中边权为 $0$ 的边中形成了环就代表他们权值肯定相等。假如说 $a$,$b$,$c$ 三个点形成了环,那么我们就有如下的方程:
$$
\begin{cases}
x_b \leq x_a \\
x_c \leq x_b \\
x_a \leq x_c
\end{cases}
$$
我们就可以得到三者相等了。)
所以我们先把类型为1、3、5的边建出来跑一个tarjan,然后再建出来剩下的边跑差分约束即可。
参考代码:Luogu P3275
AcWing 362. 区间
题目链接:AcWing || LibreOJ
这一次题目没有直接给出类似于“A大于等于B+C”这样的条件,我们需要自己推出不等式组。
首先我们需要了解我们维护的是一个不可重的集合,那么集合内的每一个数最多只能出现一次。
然后我们需要满足的条件是区间内的数字的个数不小于 $c_i$ 个。
然后我们会发现,我们可以将上述两个条件转化为前缀和数组中的不等关系。
因为我们每一个数只能出现0次或1次,所以我们前缀和数组是严格非降的,且相邻两项之间最多差1。
我们如果称前缀和数组为 $s$ 的话,那么上述条件可以转化为 $s_{i-1} \leq s_i$ 和 $s_i \leq s_{i-1} + 1$ 两个不等式。
对于第二个条件,也可以转化成为前缀和数组上的不等关系。
如果我们有一个条件是“$[ a,b ]$ 这段区间内的数字不少于 $c$ 个”的话,我们可以将其转化为类似 $s_b \geq s_{a-1} + c$ 这样的不等式。
然后我们就可以愉快地跑SPFA了,最后需要输出的是前缀和数组的最后一位——$s_{50001}$。
参考代码:AcWing 362
Luogu P4878 [USACO05DEC] Layout G
题目链接:Luogu || AcWing || LibreOJ
题目保证了奶牛的编号与其在序列中的位置是相对应的,同时两个奶牛之间的距离可以是0,也就是说我们每一个奶牛的坐标一定大于等于其上一只的坐标。
然后还有两种其他的条件,一是两头奶牛之间的距离不大于某个数,二是两头奶牛之间的距离不小于某个数。假设我们这两头奶牛分别是a和b,这个给定的数是c,那么我们对于上面两个条件分别可以得出 $x_b \leq x_a + c$ 和 $x_b \geq x_a + c$ 这两个不等式。
然后就建图跑就可以了。
参考代码:Luogu P4878