true
Cow Neighborhoods
USACO 2008 OPEN Gold
省选/NOI-
#9d3dcf
看到这一题的时候我感觉非常熟悉。
这不就是[JSOI2010]部落划分吗!
只不过这道题给定了奶牛之间的距离,并且是让求连通块的个数以及最大连通块的大小。
(可能只有我一个人觉得很类似罢)
然后做了一发,T了。
一看数据范围:$N \leq 10^5$。
秉承着“N方过百万,暴力碾标算”的精神,我认为是常数的问题加上复杂度跑满,于是就做了一些小小的优化:
首先,我将每一个坐标按照横坐标为第一关键字,纵坐标为第二关键字进行了一发排序。
因为我们不关心节点的编号,所以我们可以直接排序。
然后,我将原题中的曼哈顿距离转变为了切比雪夫距离,从而不让算法跑满。
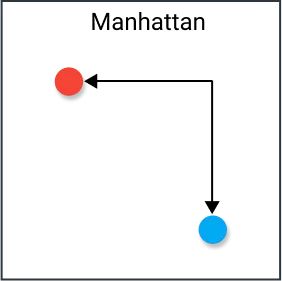
这是曼哈顿距离,其在 $k$ 维空间中的定义为:
$$
Dis(x,y) = \sum_{i=1}^k |x_i-y_i|
$$
放到二维平面里面就是 $Dis(u,v) = |x_u-x_v|+|y_u-y_v|$。
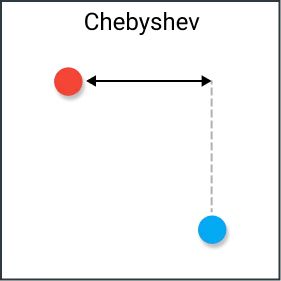
这是切比雪夫距离,其在 $k$ 维空间中的定义为:
$$
Dis(x,y) = \max_{i=1}^k |x_i-y_i|
$$
放到二维平面里面就是 $Dis(u,v) = \max(|x_u-x_v|,|y_u-y_v|)$。
如果我们将曼哈顿距离转化为了切比雪夫距离的话,就可以利用单调队列来取出 $[x-c,x+c]$ 的一段来,并在其中进行判断并连边即可,可以减小算法复杂度。
怎么转化呢?
我们考虑对于某一个点距离为定值的点构成的集合。
我们设这个点是原点 $(0,0)$,这个距离为 $c$。
当这个距离是曼哈顿距离的时候,我们这些点构成的集合就是一个倾斜了$45^{\circ}$的正方形,顶点分别为 $(0,c)$,$(c,0)$,$(0,-c)$,$(-c,0)$。
当这个距离是切比雪夫距离的时候,我们这些点构成的集合就是一个正方形,顶点分别为 $(c,c)$,$(c,-c)$,$(-c,-c)$,$(-c,c)$。
然后我们就可以发现,我们将曼哈顿距离下的这个正方形旋转$45^{\circ}$并扩大$\sqrt{2}$倍之后就是切比雪夫距离下的这个正方形。
对于一个点的情况下,我们将其坐标变为 $(x+y,x-y)$,可以达到同样的效果。
最后试了一发,T了。
看来N方还是过不了十万。
尝试减小连边的次数,我们可以尝试只连线性级别的边。
对于每一个点,我们只考虑与其左边的点连边。
同时,每一个点我们最多只连两条边,这在保证了联通性的前提下大幅度减少了连边的次数。
连哪两个点呢?
纵坐标与当前点最接近的两个即可。
其中一个在当前点上方,一个在当前点下方。
考虑正确性。
因为其他边都是冗余的,所以只连这两条边即可。
对于任意两者均可触及的点,两点向其连边之后得到的是一个三角形;
又因为当前点较靠后,所以我们可以断开当前点与其连结的边,这样也能保证连通性。
证毕。
然后就是考虑如何快速找到与当前点纵坐标最接近的两个点。
我们可以使用set来维护,使用lower_bound()来进行查找。
我们记录当前set维护的左端点,并尝试将其右移,直到左端点所对应的点与当前点的切比雪夫距离不超过 $c$。
然后就可以使用lower_bound()查找了,找到对应的节点之后连边即可。
最后要把当前节点加入set中。
交一发,过了。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| #include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 200010;
template <typename T>
inline T read()
{
T x = 0, f = 1; char c = getchar();
while(!isdigit(c)) { if(c == '-') f = -f; c = getchar(); }
while(isdigit(c)) x = x * 10 + c - 48, c = getchar();
return x * f;
}
int n;
ll c;
struct Node
{
ll x, y;
bool operator < (const Node &a) const
{
return x == a.x ? y < a.y : x < a.x;
}
}a[N];
int p[N];
int find(int x)
{
if(p[x] != x)p[x] = find(p[x]);
return p[x];
}
int sum[N];
int main()
{
n = read<int>(), c = read<ll>();
for(int i = 1; i <= n; i++)
{
ll x = read<ll>(), y = read<ll>();
a[i] = { x + y,x - y };
p[i] = i;
}
sort(a + 1, a + 1 + n);
set< pair<ll, int> >s;
set< pair<ll, int> >::iterator it;
s.insert(make_pair(a[1].y, 1));
s.insert(make_pair((1ll << 60), 0));
s.insert(make_pair((-1ll << 60), 0));
for(int i = 2, l = 1; i <= n; i++)
{
while(a[i].x - a[l].x > c)
{
s.erase(make_pair(a[l].y, l));
l++;
}
it = s.lower_bound(make_pair(a[i].y, 0));
if(it->first - a[i].y <= c)
{
int j = it->second;
int pa = find(i), pb = find(j);
if(pa != pb)p[pa] = pb;
}
it--;
if(a[i].y - it->first <= c)
{
int j = it->second;
int pa = find(i), pb = find(j);
if(pa != pb)p[pa] = pb;
}
s.insert(make_pair(a[i].y, i));
}
int cnt = 0, maxn = 0;
for(int i = 1; i <= n; i++)
{
cnt += (find(i) == i);
maxn = max(maxn, ++sum[find(i)]);
}
printf("%d %d\n", cnt, maxn);
return 0;
}
|

