true
星座 3
JOISC 2020 Day3 T1
省选/NOI-
#9d3dcf
- Luogu P7219
- LibreOJ #3277
- UOJ #507
对于这道题来说,我们有两种做法。
首先我们可以确定一点,就是他给我们的建筑是一定到底的,那么肯定不是让我们从左往右枚举的。
这里就以样例来举个例子:

我们首先看最上面的这一行。
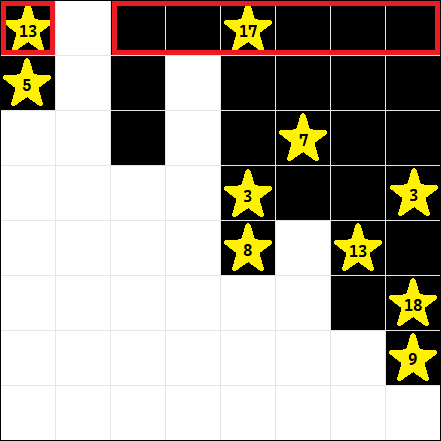
当我们碰到了最高的那个建筑的时候,我们当前这个区间就被分成了两份。

随着我们不断向下,我们的区间也在不断细分,直到最后全是建筑。
然后我们就可以以此建立一棵笛卡尔树了。
其中我们的根节点是最上面的那一行再往上的那一片空白区域,我们可以保证其一定是一个完整的区间。
对于每一个区间,我们需要先处理一下,使其只剩一颗星星。
这样可以大大简化我们的冲突判断,减少了对时间的需求。
其次,我们需要对两个(或多个)区间进行合并,就好似对这个区间进行DP,让每一个区间中的那一颗星星选或不选,然后如果选的话就考虑其下面与其冲突的星星,这样这个区间的子树的所有星星都需要删去。
这样一直合并到最上面的区间之后就得到了我们要的结果。
我们可以使用树链剖分来维护上面的信息。
不过下面有个更优的做法,就不放代码了。
我们可以贪心一下。
首先我们将所有房屋和星星按照纵坐标从小到大排个序。
然后我们搞一个并查集,使用并查集维护每一个点可以到达的最大范围。
最后我们建立一棵树状数组,用来存储每一个横坐标中把所有星星清空的代价之和。这一棵树是随着枚举纵坐标不断更新的。
之后我们从下往上处理信息。
对于每一个纵坐标,我们假设已经处理出来所有纵坐标小于其的答案。
我们在树状数组上面查找当前纵坐标所对应的值 $S$,与消除这一颗星星所需要的代价 $C$ 比较一下。
- 如果 $S \geq C$,那就意味着我们加入这颗星星并不会使答案更优,因为靠上的星星可能会冲突的概率更大一些,况且保留其权值又不如保留其下面的星星的权值之和更优。所以我们的答案直接加上 $C$ 即可。
- 如果 $S < C$,那我们就不能确定保留这一颗星星是否更优了。我们先暂且给答案加上 $S$,然后将当前星星能够到达的横坐标上的每一个值加上 $C-S$。这样我们在继续枚举的时候如果发现留着当前点仍然不优,那么我们就向答案里面又加入了 $C-S$,相当于是向答案中加入了 $C$,而把 $S$ 拎了出来。
前者的正确性很显然,后者则可以这样想:
我们已经在递推的时候的每一步都是当前纵坐标的最优解,而我们保留 $C$ 相当与就是舍弃了这个最优解。
当我们再想把 $C$ 删去而保留 $S$ 的时候,选取的 $S$ 仍然是那个区间的最优解,就不需要继续考虑更深的点了。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 200010;
struct dsu
{
int p[N];
int find(int x)
{
if (p[x] != x)p[x] = find(p[x]);
return p[x];
}
}L, R;
int n, m;
#define lowbit(x) (x&-x)
ll tr[N];
void add(int x, ll c)
{
for (int i = x; i <= n; i += lowbit(i))
tr[i] += c;
}
ll sum(int x)
{
ll res = 0;
for (int i = x; i; i -= lowbit(i))
res += tr[i];
return res;
}
ll ans;
vector<pair<int, int> >st[N];
vector<int>h[N];
int main()
{
scanf("%d", &n);
L.p[n + 1] = R.p[n + 1] = n + 1;
for (int i = 1; i <= n; i++)
{
L.p[i] = R.p[i] = i;
int x;
scanf("%d", &x);
h[x].push_back(i);
}
scanf("%d", &m);
for (int i = 1; i <= m; i++)
{
int x, y, c;
scanf("%d%d%d", &x, &y, &c);
st[y].push_back(make_pair(x, c));
}
for (int i = 1; i <= n; i++)
{
for (pair<int, int> s : st[i])
{
ll S = sum(s.first);
if (S > s.second)ans += s.second;
else
{
ans += S;
add(L.find(s.first) + 1, s.second - S);
add(R.find(s.first), S - s.second);
}
}
for (int j : h[i])
{
L.p[j] = j - 1;
R.p[j] = j + 1;
}
}
printf("%lld\n", ans);
return 0;
}
|


