Manacher 算法

发表于 2023-02-27 分类于字符串本文字数： 1426 阅读时长 ≈ 4 分钟

一种能在 $O (n)$ 的时空复杂度内求出一个字符串内所有回文子串的算法。

在讨论任何问题之前，我们需要想到回文串可以按照长度分为奇数长度和偶数长度两类，其中奇数长度的串的中间位置是字符，而偶数长度的则是空隙。
为了方便讨论，我们将字符与字符之间的空隙，以及字符与字符串边界之间的空隙都用当前字符集以外的字符填充上，这样我们所有的回文串都可以转化成为中心在字符上的类型了。

首先，我们可以想到一个 $O (n^{2})$ 的朴素算法，那就是对每一个位置，不断像两边扩展，直到不能扩展为止，这样我们就会得到以每个位置为中心的极长回文子串了。

我们尝试优化这个算法。
因为我们记录下来了之前每一个位置的极长回文子串的信息，我们可以尝试利用这些信息。
比如说对于一个位置，如果其是位于一个回文串内的话，我们可以尝试利用其对称位置的信息来减少枚举次数。
比如下面这个例子：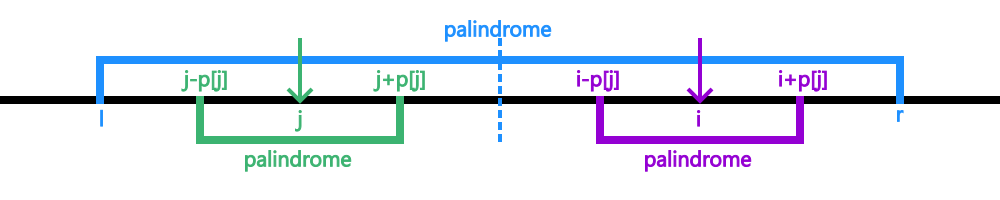

我们当前的位置是 $i$ ，这个位置在一个回文串中，范围是 $[l, r]$ 。回文串中与之对应的位置是 $j$ ，其答案已知，为 $p_{j}$ 。
因为两个位置在当前的这个大回文串中对称，那么我们就可以知道 $i$ 周围是有与 $j$ 所在回文串相对应的一个小回文串的。
以这个为基础，我们再往两边尝试扩展当前回文串，不过如果我们刚才得到的那个以 $i$ 为中心的回文串完全在 $[l, r]$ 这个大回文串内且不顶着边界的话，因为其两边会与 $P_{j}$ 的两边相对应，我们已经知道其不匹配了，这样我们就可以直接省去向两边扩展的这个过程，否则就需要继续尝试向两边扩展。

当然，还可能会出现一种特殊的情况，就是 $j$ 所在的小回文串已经出了 $[l, r]$ 的范围（也就是 $j - p_{j} < l$ ），就像下面这样：

我们知道 $P_{j}$ 在 $l$ 左边的位置是与（可能的） $P_{i}$ 在 $r$ 右边的位置是一定不匹配的（要不然我们可以延长 $[l, r]$ ），我们只能忍痛裁掉（可能的） $P_{i}$ 超过 $r$ 的那一部分：

每一次我们求出来一个位置的答案之后，我们都需要尝试更新当前作为背景的这个回文串。
我们不需要其覆盖很长，而需要其尽量靠右，为我们后面的位置做贡献。

以上面所说的内容，我们可以写出如下的代码：

vector<int>manachar(string s)
{
    int n = s.size();
    vector<int>res(n);
    for(int i = 0, l = 0, r = -1; i < n; i++)
    {
        int k = (i > r) ? 1 : min(res[l + r - i], r - i + 1);
        while((i - k >= 0) && (i + k < n) && (s[i - k] == s[i + k]))k++;
        res[i] = k--;
        if(i + k > r)l = i - k, r = i + k;
    }
    return res;
}

然后就是分析其时间复杂度了。（空间复杂度是铁定 $O (n)$ ）
乍一看，我们觉得因为其每一个位置都会尝试调用朴素算法，其时间复杂度的线性性并不显然。
不过我们需要考虑，当我们的回文串在 $[l, r]$ 内或者被 $[l, r]$ 截断的时候，我们不需要调用朴素算法，而我们每一次调用朴素算法都会更新 $[l, r]$ ，这可以把朴素算法的调用和 $r$ 的移动联系起来。
又因为 $r$ 只升不降，我们最多会让 $r$ 增加 $O (n)$ 级别的数量，那我们最多调用 $O (n)$ 次朴素算法，时间复杂度也就变成了最多 $O (n)$ 。

最后，我们需要注意一下答案的转化。
因为我们将字符串转化成了类似 $# s_{0} # s_{1} # s_{2} # \dots # s_{n - 1} # s_{n} #$ 的样子，我们的答案会与实际的回文串长度不一样。
首先，我们记录的 $d_{i}$ 是代表我们在 $[i - d_{i} + 1, i + d_{i} - 1]$ 这个区间内有一个极长的回文串。
那么长度应该为奇数的字符串转化后就形如 $# a # b # c # b # a #$ ，实际长度应该是 $d_{i} - 1$ ；长度应该为偶数的字符串转化后就形如 $# a # b # b # a #$ ，实际长度也应该是 $d_{i} - 1$ 。

以上所说的算法就是所谓的 Manacher 算法，由 Glenn K. Manacher 提出和得名。